pattern lock

前几天和一朋友聊到手机解锁, 朋友问我有没有想过手机pattern lock有多少种组合方式. 其实这个问题早就想过了, 以前感觉会有很多种特殊情况, 用程序解还不如用排列组合来得快

后来讨论了下, 就决定把问题简化: 只考虑4个点或4个点以上的情形, 并且包含下图这种路径的不算有效的组合方式

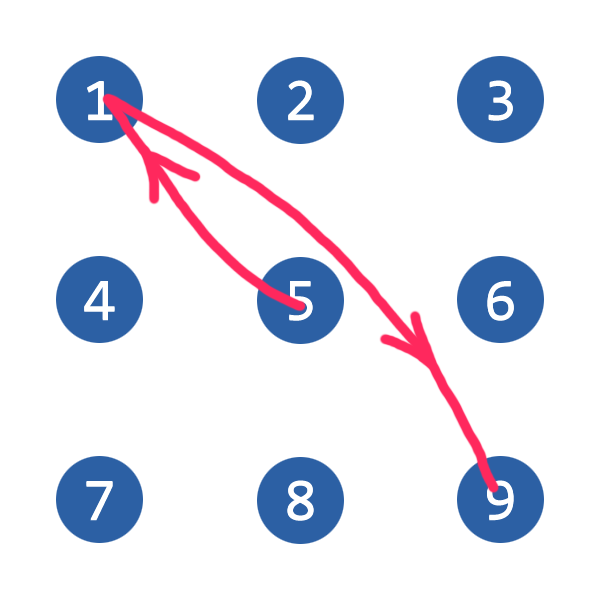
用回溯写了个解

#define N 4

typedef struct
{
    char *pa;
    char *pn;
} point_info;

int x[10] = {0};
point_info points[10];

void init_points()
{
    points[0].pa = "x1x2x3x4x5x6x7x8x9";
    points[0].pn = "";
    points[1].pa = "x2x4x5x6x8";
    points[1].pn = "x3x7x9";
    points[2].pa = "x1x3x4x5x6x7x9";
    points[2].pn = "x8";
    points[3].pa = "x2x4x5x6x8";
    points[3].pn = "x1x7x9";
    points[4].pa = "x1x3x5x6x7x8x9";
    points[4].pn = "x6";
    points[5].pa = "x1x2x3x4x6x7x8x9";
    points[5].pn = "";
    points[6].pa = "x1x2x3x5x7x8x9";
    points[6].pn = "x4";
    points[7].pa = "x2x4x5x6x8";
    points[7].pn = "x1x3x9";
    points[8].pa = "x1x3x4x5x6x7x9";
    points[8].pn = "x2";
    points[9].pa = "x2x4x5x6x8";
    points[9].pn = "x1x3x7";
}

int last_ele(point_info *p)
{
    char *str = p->pa;
    return *(str + strlen(str) - 1);
}

int last_ele(point_info *p)
{
    char *str = p->pa;
    return *(str + strlen(str) - 1);
}

int next_ele(point_info *p, int e)
{
    char *str;
    int i;

    str = p->pa;

    if(0 == e)
        return *str;

    for(i = strlen(str) - 1; i > 0; --i, ++str)
        if(*str == e)
            return *(str + 1);

    return *str + 1;
}

int correct(int p)
{
    int i;
    for(i = p - 1; i > 0; --i)
        if(*(x + i) == *(x + p))
            return 0;
    return 1;
}

void print_ans(int leng)
{
    int i = 1;
    for (; i <= leng; ++i)
        printf("%d", *(x + i));
    printf("n");
}

int back_track(int leng)
{
    int count = 0, p = 1;
    while (p > 0)
    {
        point_info *pre = points + x[p - 1];
        x[p] = next_ele(pre, x[p]);
        while(!correct(p) && x[p] <= last_ele(pre))
            x[p] = next_ele(pre, x[p]);
        if(x[p] > last_ele(pre))
        {
            x[p] = 0;
            --p;
        }
        else
        {
            if(p != leng)
                ++p;
            else
                ++count;
        }
    }
    return count;
}

int main(int argc, char **argv)
{
    int i = 4, count = 0, tmp;
    init_points();
    for(; i < 10; ++i)
    {
        tmp = back_track(i);
        printf("%dn", tmp);
        count += tmp;
    }
    printf("%dn", count);
    return 0;
}

写得有点quick dirty, 得出的答案是140045, 不知道对不对
先放这里, 抽空再研究研究